Codeforces Global Round 14 F – Phoenix and Earthquake 解説

前書き

Codeforces に出題されたグラフの問題がまた解けなかったので記事にします。

問題概要

問題へのリンク

\(N\) 頂点 \(M\) 辺の無向グラフが与えられる。各頂点には重み \(a_i\) が与えられている。初め、どの辺も利用されておらず、\(N\) 個の孤立点からスタートする。
「辺を１つ選び採用する（端点が同じ連結成分に所属していてはいけない）。端点を辺によって繋いだ後に、その連結成分の重みから \(x\) をマイナスする（ \(x\) 未満ならその操作はできない）。」という操作を考える。操作を \(N-1\) 回行って、全域木を作れるか？作れる場合はその手順も示せ。

制約

\(1 \le N \le 3 \times 10^5\)
\(1 \le M \le \min(N-1,3 \times 10^5)\)
\(1 \le x \le 10^9\)

考えたこと

（本質でもなんでもないのだが、）以下のように問題を変える。

変える前：「両方の頂点の重みの合計が \(x\) 以上なら辺を張れる。張った後、重みを \(x\) 減らす。」

変える後：「入力で受け取る \(a_i\) の値を \(a_i – x\) に変換する。両方の頂点の重みの合計が \(-x\) 以上なら辺を張れる。」

変換後では重みをいちいち減らす必要がなく、また、証明の記述が若干楽かもしれない。

詳細な解答

公式解説へのリンク

※公式解説を参考にして記述していますが、内容は少し違います。

まず、 \(a_i\) の合計が \(-x\) 未満であるなら、答えは自明に NO である。さて、YESである場合の条件は非自明だが、実はそうでない場合は YES になる。（このように、簡単に見える事実の裏が実は成り立つ、というのは競技プログラミングでは良く見る光景のように思う。）

（証明）さて、本来なら厳密に帰納法に則って証明するが、問題を変換したため操作可能な条件が \(N\) に非依存な形に書き換わった。そのため、より直感的な説明をここでは与える。

頂点の値が \(a_1 \le a_2 \le a_3 \le … a_n\) と昇順に並んでいるとする。今ここでは、

\(-x \le a_1 + a_2 + a_3 + … a_n\) … (1)
\(-x \le a_1 \le a_2 \le a_3 \le … a_n\) … (2)

の２つが成立しているが、この時、 \(-x \le a_1 + a_n\) も成立する。理由は、\(0 \le a_n\) ならば \(-x \le a_1 \le a_1 + a_n\) であり、\(0 \gt a_n\) なら、\(a_1 + a_n \ge -x – a_2 – a_3 – … a_{n-1} \ge -x\) が成り立つからである。

(1) (2) の両条件がどの操作後も成り立つので、繰り返すことで全域木を作ることが可能である。（証明終）

以上の観察から、「最大値を持つ頂点の持つ辺を見て、どれかを採用する」という操作を繰り返せば良い。

この処理を実装しようとすると、辺を採用して頂点を縮約する処理が必要で、これについては、以下の図のように辺をまとめれば良い。

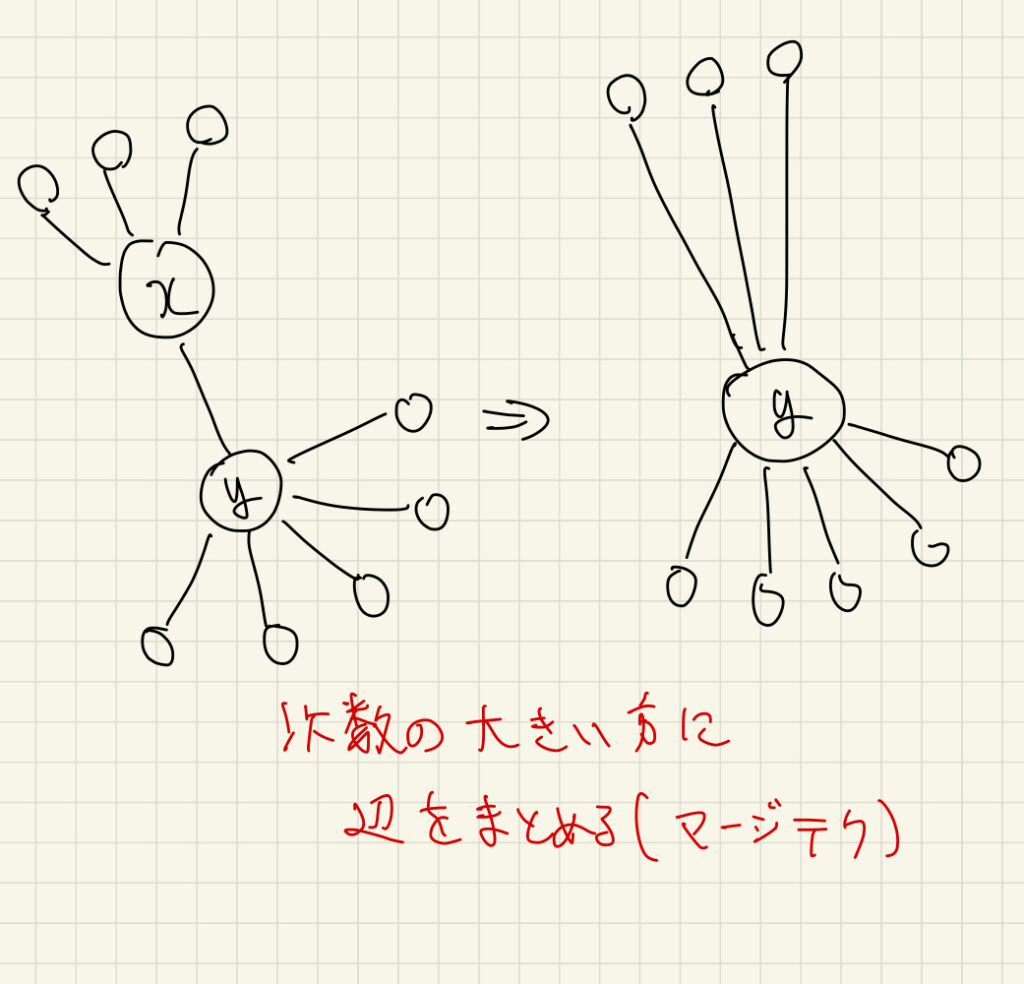
他にも、辺をまとめる際には、vector の末尾に追加し、辺を見る際には後ろから見て、同じ連結成分に属していた場合（＝縮約される辺）は pop_back() により辺を削除する処理を追加するとACした。

// 縮約処理の内容 (while文の中身)

while (true) {
        auto [w, v] = *pq.rbegin();
        // 辺を後ろから見る
        for (int i = G[v].size() - 1; i >= 0; i--) {
            auto [u, edge] = G[v][i];
            // 同じ連結成分の場合
            if (same(u, v)) {
                // 辺を削除する
                G[v].pop_back();
                continue;
            }
            // priority_queue の削除
            pq.erase(P(size(u), find(u)));
            pq.erase(P(size(v), find(v)));

            unite(u, v, 1);
            ans.pb(edge);

            // priority_queue へ追加
            pq.insert(P(size(find(u)), find(u)));
            break;
        }
        if (ans.size() == n - 1) break;
    }

// 縮約処理の内容 (while文の中身)

while (true) {

auto [w, v] = *pq.rbegin();

// 辺を後ろから見る

for (int i = G[v].size() - 1; i >= 0; i--) {

auto [u, edge] = G[v][i];

// 同じ連結成分の場合

if (same(u, v)) {

// 辺を削除する

G[v].pop_back();

continue;

}

// priority_queue の削除

pq.erase(P(size(u), find(u)));

pq.erase(P(size(v), find(v)));

unite(u, v, 1);

ans.pb(edge);

// priority_queue へ追加

pq.insert(P(size(find(u)), find(u)));

break;

}

if (ans.size() == n - 1) break;

}

反省

存在しない入力を考えて解法を棄却したこと
- \(-x \le a_i\) の条件を忘れていて、その結果全域木を取るだけでは解決しないケースを考えていた。
実装
- マージテクの部分で別の変数（次数ではなくてサイズ）を見ていた。
- 同じ連結成分の辺を削除する処理を思いつくのに時間がかかった。