AtCoder AGC 053 C – Random Card Game 解説記事

問題概要

問題へのリンク

\(1\) から \(2N\) までの番号が付いたカードがあり、カードを \(N\) 枚からなる \(2\) つの山にランダムに分ける。「両方の山の上から \(k\) 枚目同士を比較して、小さい方を取り除く」という操作を考えるとき、片方の山が空になるまでの操作回数をスコアと呼ぶ。スコアを最小化するようにプレイするとき、その期待値を求めよ。

制約

\(1 \le N \le 10^6\)

解答の指針

この問題に必要なステップを要約すると以下のような感じ。

スコアがどういう値になるのか、その性質についての考察
数えやすくするためのちょっとした工夫
典型的な順列の数え上げに対する手法の適用
ad-hoc な高速化

詳細な解答

公式解説へのリンク

1. プレイ戦略

まず、\(2N\) 番のカードを取り除くことはできない。よって、カードが残るのは \(2N\) 番のカードが存在する方の山になる。よって、「スコア を最小化するようにプレイ」＝「\(2N\) 番のカードがある山の方に出来るだけカードを残して終わらせるようにプレイ」ということが分かる。以降では、\(2N\) 番のカードが存在する山を B として、そうでない山を A とする。

2. スコアの考察 1 （スコアをNに出来るか？）

さて、スコアの最適値は \(N\) である。この値を達成できる条件について考えよう。

このとき、Bのカードを \(1\) 枚も消費できないため、\(A_1\) は \(B_1\) に消してもらうしかない。

次に、\(A_2\) については、

\(A_1\) を先に消す場合 — \(B_1\) に消してもらうしかない。
\(A_2\) を先に消す場合 — \(B_2\) に消してもらうしかない。

となり、\(\max(B_1, B_2) \gt A_2\) という条件を満たす必要があることが分かる。以降同様に、\(\max(B_1, B_2, \ldots, B_i) \gt A_i\) という条件を全ての \(i\) について満たせば良いことがわかる。

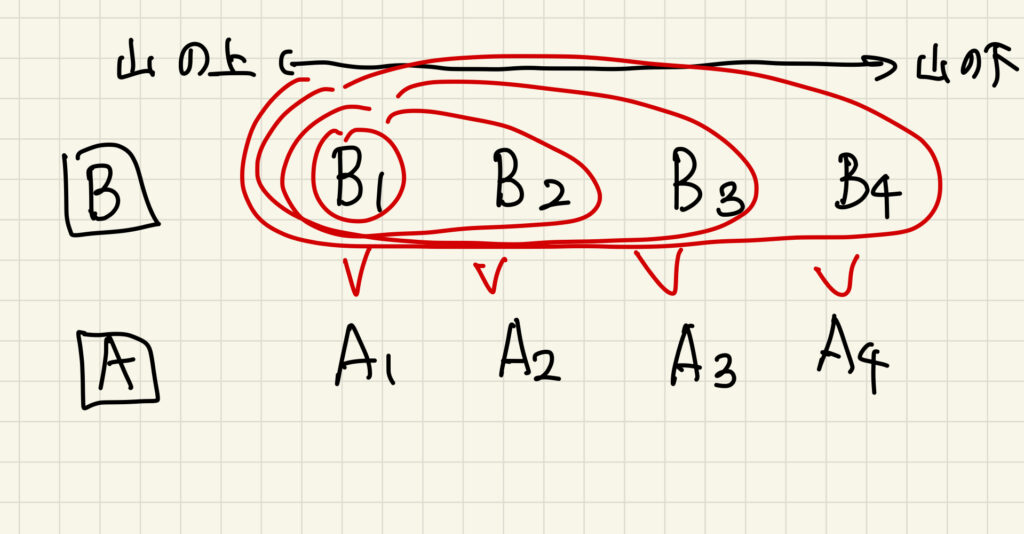
3. スコアの考察 2 （スコアの値は幾つになるか？）

スコアの値が実際にいくつになるのかを考える。

Aの山のカードから見た時、「自分より大きいカードで、一番上（図だと、一番左）にあるものがどこにあるか？」を考えて、矢印を引く（図２）。このとき、「一番長い右向きの矢印の長さ」が「必要なBの消費するカードの枚数（＝スコア \( – N\)）」となる。（厳密な証明は省略するが、「スコアがこの値以上になること」と「実際にこのスコアが達成な操作手順が存在すること」を示せば良い。）

4. 数え上げ

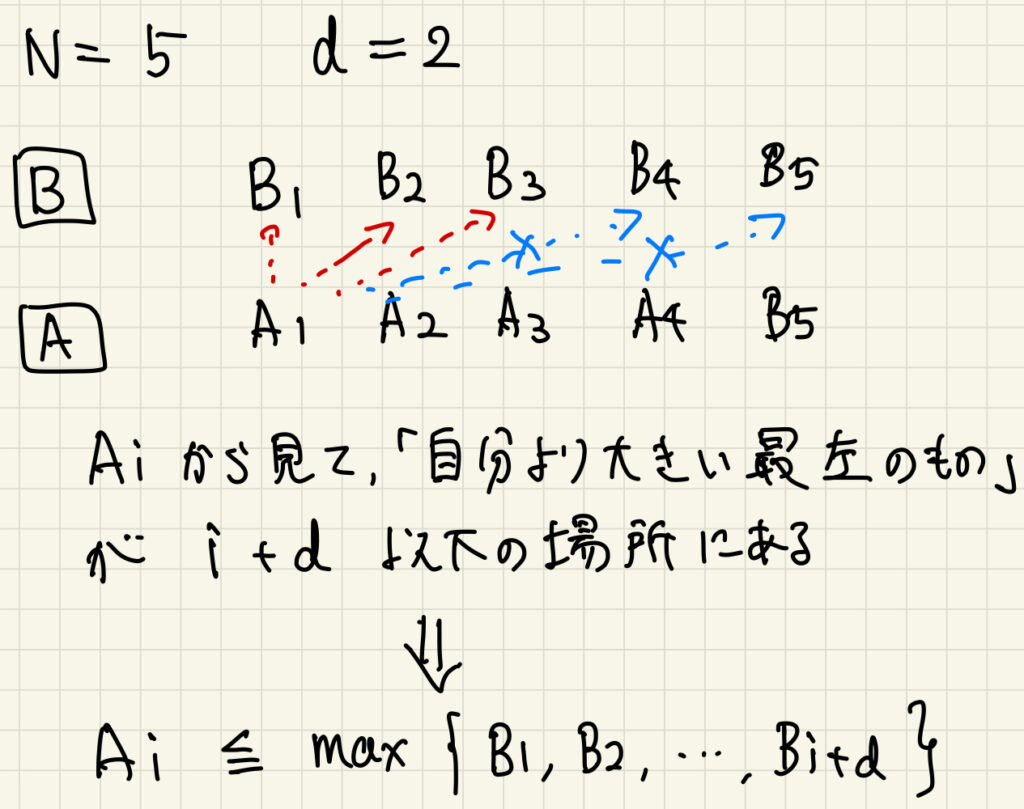
「矢印の長さの最大値」を管理するのは難しいので、「矢印の長さを \(d\) 以下に抑える」場合を考えて、差分を用いて計算する（典型）。

この時の条件を観察すると、\(A_i \le \max(B_1, B_2, \ldots, B_{i+d})\) となる（図３）。

さて、この条件を満たす順列を数え上げるために、「挿入DP」の適用を考える。（今回はDPではないが、便宜上こう呼ぶことにする。）挿入DPには、以下の \(2\) 種類あると考えている。

「位置関係」に対して挿入する。（例：大きい順に見て、どの場所に挿入するかを考える）
「大小関係」に対して挿入する。（例：左から見て、どの要素を挿入するかを考える）

今回はこれらのうちの \(2\) つ目を使うことを考える。（本当はこの \(2\) 種類を区別する必要なんてないのだが、このほうが分かりやすいかな？と考えたためこういう表記をしている。かえって分かりづらい、という人は無視してください。）

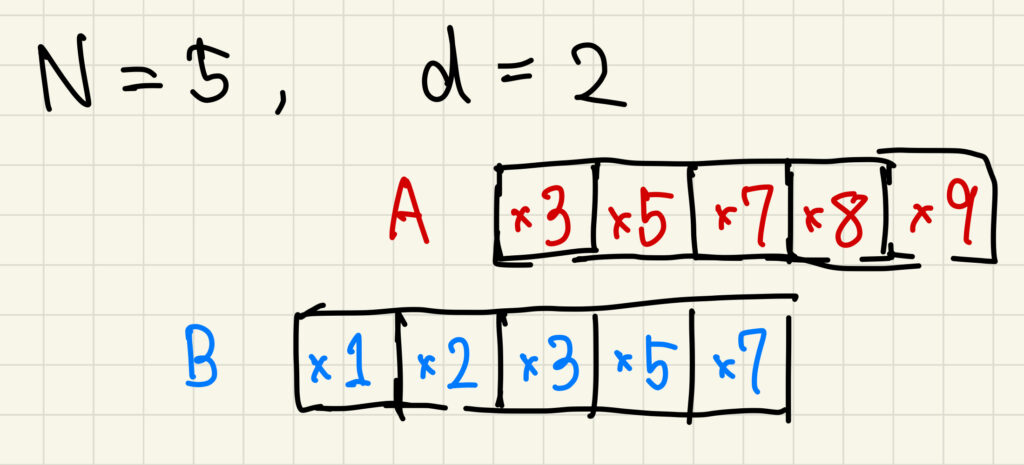
条件の式に注目して、以下のような順序（図４）で要素を挿入することを考える。

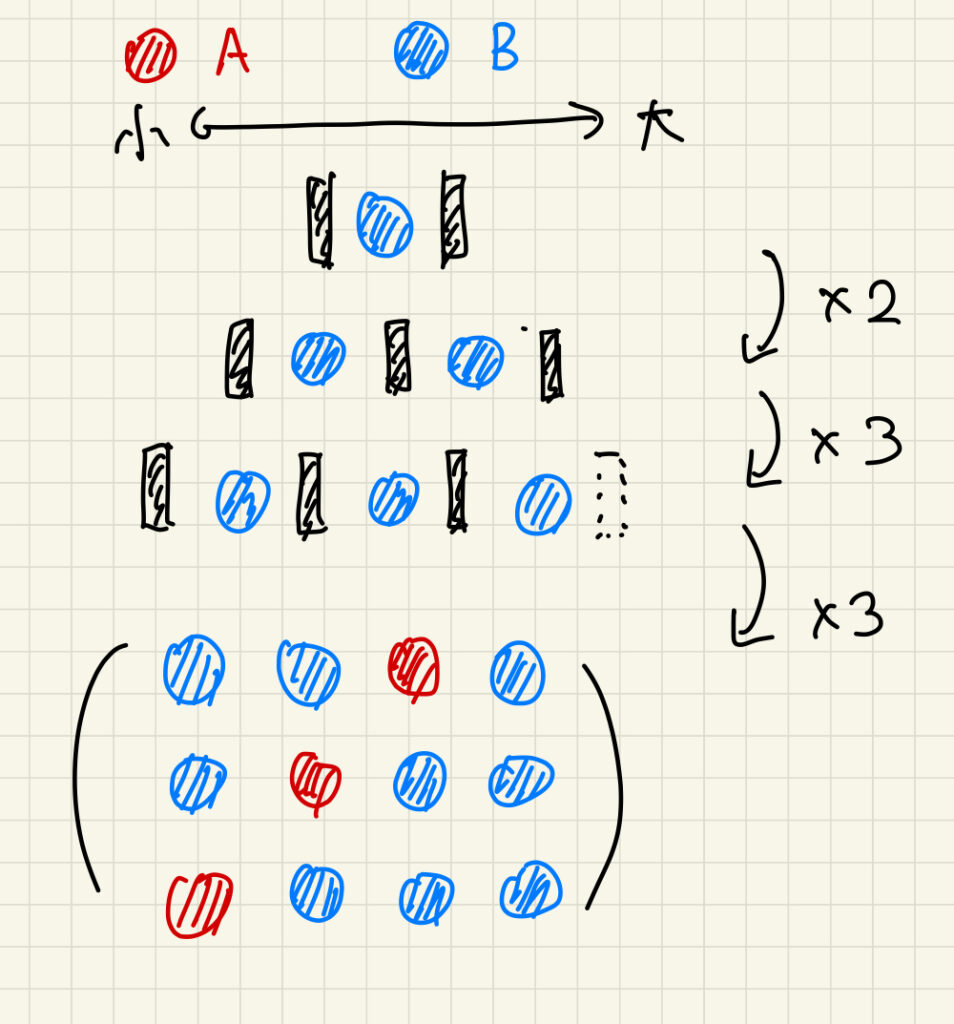
各挿入のタイミングで、どの要素を挿入できるかを考える。B に要素を挿入する場合は特に制約を考えないため、「（現在の要素数）＋１」を掛ければ良い。A に要素を挿入する場合は、その時点での最大値を挿入することが出来ないため、「（現在の要素数）」を掛ければ良い。（図５・図６）

ここまでの議論に沿うことで、\(O(N^2)\) のコードを書くことが出来る。あとはこれを適切に高速化（高速化については、そんなに難しくないので省略）すれば、ACできる。

コード

#include <atcoder/modint>
#include <bits/stdc++.h>

using namespace atcoder;
using namespace std;
using mint = modint1000000007;

typedef long long ll;

mint dp[1000005];

int main() {
    ll n;
    cin >> n;
    for (int d = 0; d < 2; d++) {
        // 矢印の長さを d 以下に抑えた場合の数
        // 　（＝スコアが N + d 以下になる場合の数）
        // dp[0] と dp[1] は真面目に計算
        mint res = 1, a = 1;
        for (int i = 0; i < d; i++) {
            res *= a;
            a += mint(1);
        }
        for (int i = 0; i < n - d; i++) {
            res *= a * a;
            a += mint(2);
        }
        a -= mint(1);
        for (int i = 0; i < d; i++) {
            res *= a;
            a += mint(1);
        }
        dp[d] = res;
    }
    for (int d = 2; d < n; d++) {
        // dp[d - 2] の値を用いて、dp[d] の値を高速に計算する
        dp[d] = dp[d - 2] * mint(d) * mint(2 * n - d);
        dp[d] /= mint(d - 1) * mint(2 * n - d + 1);
    }
    // 差分を計算
    for (int d = n - 1; d >= 1; d--) {
        dp[d] -= dp[d - 1];
    }
    mint ans = 0;
    // スコアの総和を計算
    for (int d = 0; d < n; d++) {
        ans += dp[d] * mint(n + d);
    }
    ans *= mint(2);
    for (int i = 1; i <= 2 * n; i++) {
        ans /= mint(i);
    }
    cout << ans.val() << endl;
}

#include <atcoder/modint>

#include <bits/stdc++.h>

using namespace atcoder;

using namespace std;

using mint = modint1000000007;

typedef long long ll;

mint dp[1000005];

int main() {

ll n;

cin >> n;

for (int d = 0; d < 2; d++) {

// 矢印の長さを d 以下に抑えた場合の数

// 　（＝スコアが N + d 以下になる場合の数）

// dp[0] と dp[1] は真面目に計算

mint res = 1, a = 1;

for (int i = 0; i < d; i++) {

res *= a;

a += mint(1);

}

for (int i = 0; i < n - d; i++) {

res *= a * a;

a += mint(2);

}

a -= mint(1);

for (int i = 0; i < d; i++) {

res *= a;

a += mint(1);

}

dp[d] = res;

}

for (int d = 2; d < n; d++) {

// dp[d - 2] の値を用いて、dp[d] の値を高速に計算する

dp[d] = dp[d - 2] * mint(d) * mint(2 * n - d);

dp[d] /= mint(d - 1) * mint(2 * n - d + 1);

}

// 差分を計算

for (int d = n - 1; d >= 1; d--) {

dp[d] -= dp[d - 1];

}

mint ans = 0;

// スコアの総和を計算

for (int d = 0; d < n; d++) {

ans += dp[d] * mint(n + d);

}

ans *= mint(2);

for (int i = 1; i <= 2 * n; i++) {

ans /= mint(i);

}

cout << ans.val() << endl;

}

反省点

誤読したこと
- 「スコアの最小化」じゃなくて「スコアの最大化」だと思って解いていた。今回はCにあまり時間をかけていなかったためあまり実害は無かったが、焦りすぎずしっかりと問題文を読むように心がける。（特に、AGCは英語問題文を日本語訳している（多分だけど）ので不自然な日本語も多い。）
挿入DPに対する苦手意識があった
- 挿入DPの問題は解いたことがあったが、（記事中で言うところの）「位置関係に対する挿入」にしか意識していなかった。
- 大小関係にもっと注目すべき。\(d\) 個ずらして数字を配置していく方法も、条件をしっかり大小関係の形に表してから考察すれば思いついていてもおかしくないかもしれない。

AtCoder AGC 053 C – Random Card Game (900点)