AtCoder ARC 036 C – 偶然ジェネレータ

問題概要

問題へのリンク

0, 1, ? からなる \(N\) 文字の文字列が与えられる。? に 0 か 1 を記入して、「どの連続部分列も、0と1の個数差が \(K\) 以下になる」という条件を満たす方法は何通りあるか？

制約

\(1 \le K \le N \le 300\)

解答

公式解説へのリンク

1. まずは判定問題

数え上げの問題では、まず判定問題を考えることで方針が浮かぶ可能性がある。今回では「個数差が最大になる連続部分列について、その個数差はいくつか？」という問題を考える。

まず０を−１にして考える。連続部分列に関する問題なので、初項からの合計を考える。この時、最大の個数差は、「合計値のうち最大のものから最小のものを引いたもの」になる（図１）。

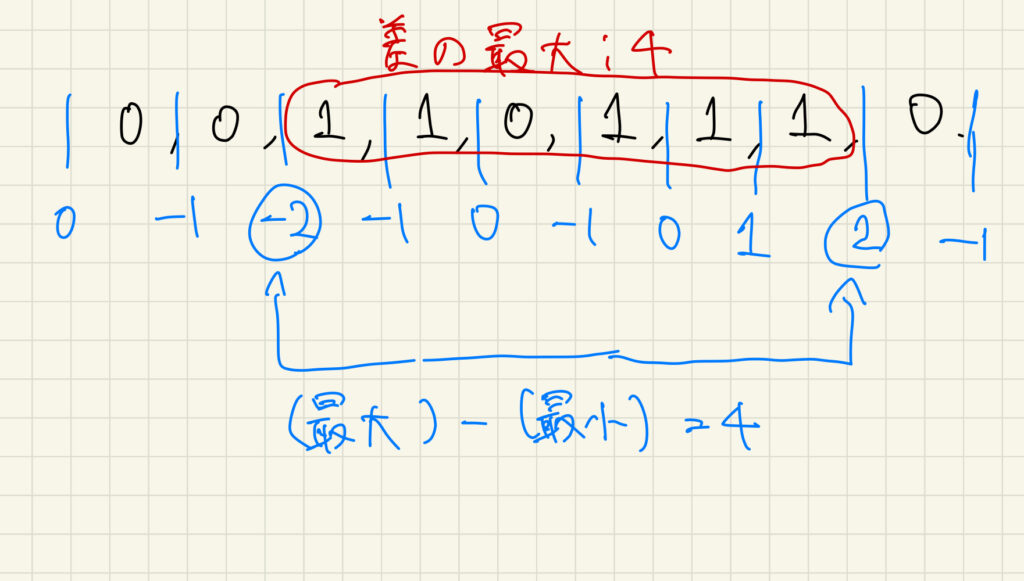
2. DP

「合計値のうち最大値 – 最小値が \(K\) 以下になる」という条件は扱いにくいため、最小値を固定（ここでは \(L\) とする）して、「合計値が \(L\) 以上 \(L + K\) 以下になる」という条件に変換して考える。これは単純なDP（DP[i][j] := i 文字目まで見て、合計値が j となる場合の数）を適用し、\( L \le j \le L + K\) の範囲外には遷移しないことで求めることができる。

しかしこれでは、重複が発生してしまう。重複を取り除くために、ここでは「最小値（＝L）を達成した瞬間があるか？」をDPの引数として持たせることで、重複をなくすことができる。

コード

// 解答
bool solve() {
    cin >> n >> k;
    cin >> s;
    ll ans = 0;
    for (int i = -k; i <= 0; i++) {
        // [mini, maxi] の範囲でのみ遷移する
        ll mini = i + 300, maxi = i + k + 300;

        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= 600; j++) {
                dp[i][j][0] = dp[i][j][1] = 0;
            }
        }

        dp[0][300][(mini == 300) ? 1 : 0] = 1;

        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= 600; j++) {
                for (int k = 0; k < 2; k++) {
                    if (s[i] != '1' && j > mini) {
                        // 0 を使う場合
                        int newk = (j - 1 == mini) ? 1 : k;
                        dp[i + 1][j - 1][newk] += dp[i][j][k];
                        dp[i + 1][j - 1][newk] %= mod;
                    }
                    if (s[i] != '0' && j < maxi) {
                        // 1 を使う場合
                        dp[i + 1][j + 1][k] += dp[i][j][k];
                        dp[i + 1][j + 1][k] %= mod;
                    }
                }
            }
        }

        for (int i = 0; i <= 600; i++) {
            ans += dp[n][i][1];
            ans %= mod;
        }
    }
    cout << ans << endl;
    return true;
}

// 解答

bool solve() {

cin >> n >> k;

cin >> s;

ll ans = 0;

for (int i = -k; i <= 0; i++) {

// [mini, maxi] の範囲でのみ遷移する

ll mini = i + 300, maxi = i + k + 300;

for (int i = 0; i <= n; i++) {

for (int j = 0; j <= 600; j++) {

dp[i][j][0] = dp[i][j][1] = 0;

}

dp[0][300][(mini == 300) ? 1 : 0] = 1;

for (int i = 0; i < n; i++) {

for (int j = 0; j <= 600; j++) {

for (int k = 0; k < 2; k++) {

if (s[i] != '1' && j > mini) {

// 0 を使う場合

int newk = (j - 1 == mini) ? 1 : k;

dp[i + 1][j - 1][newk] += dp[i][j][k];

dp[i + 1][j - 1][newk] %= mod;

}

if (s[i] != '0' && j < maxi) {

// 1 を使う場合

dp[i + 1][j + 1][k] += dp[i][j][k];

dp[i + 1][j + 1][k] %= mod;

}

for (int i = 0; i <= 600; i++) {

ans += dp[n][i][1];

ans %= mod;

}

cout << ans << endl;

return true;

}