問題概要
数列 \((1, 2, \cdots, n)\) に対して、「項を \(1\) つ選んで、それを先頭か末尾に移動させる」という操作を \(m\) 回繰り返すと、 \((a_1, \cdots, a_n\)) になった。\(m\) 回の操作列としてありうるものの総数を \(\bmod 998244353 \) で求めよ。
制約
- \( 2 \le n \le 3000 \)
- \( 1 \le m \le 3000 \)
- \(( a_1, \cdots, a_n) \) は \(( 1, \cdots, n) \) の順列
解答の指針
- 「数列に対して、要素を選び、場所を移動させる」という操作が登場するこの手の問題では、「ある要素を動かす最後の操作か / 最後の操作ではないか」が重要になることが多いイメージ。
- 今回の問題では、そのような「最後の操作をされた要素」たちは両端に並ぶことになり、個数が決まればその要素たちの値が決まるのがポイント。
- また、「最後の操作」はある意味で破壊的操作(もうそれ以上その要素に操作はできない)なので、逆順に見ると有効であるのではないかと考えられる。
詳細な解答
※ほとんど公式解説と同じです
動的計画法の適用を考える。\( dp[i][L][R] := i\) 回の操作を行なったとき、「最後の操作をされた要素」が右側に \(R\) 個、左側に \(L\) 個並ぶような操作列の個数 、とする。
さて、\( dp[i][L][R] \) の計算方法について考える。\( i \) 回の操作のうち \(1\) 回目の操作は、次のうちのどれかである。
- 右に要素を動かして、その要素にはもう操作しない。
- 左に要素を動かして、その要素にはもう操作をしない。
- 右に要素を動かすが、その要素にはまた操作をする。
- 左に要素を動かすが、その要素にはまた操作をする。
1番と2番は比較的簡単で、それぞれ \(dp[i-1][L][R-1], dp[i-1][L-1][R]\)である。3番と4番について、また操作をしなくてはいけないということに注目して、「どの要素を動かすか」ではなく「その要素に最後の操作をするのが今後の操作の何回目か」という考え方をして係数を計算する。(最後に操作をするのが、左 or 右の中で何回目に当たるのかがわかれば自然と動かす要素も定まる。)するとどちらも \(dp[i-1][L][R] \times (L+R) \) であることがわかる。
さて、以上のDPを実行しても計算時間には間に合わない。DPの式に注目すると、この漸化式は、「\((0, 0)\) から \(i\) 手で \((L, R)\) に到達する経路数、ただし立ち止まることもできて、その場合 \(2(x + y)\) の係数がかかる」と解釈できる(図1)。
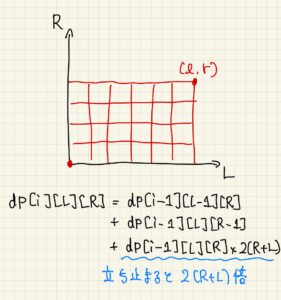
ここで\(L\) 軸に沿って移動する場合と、\(R\) 軸に沿って移動する場合を一旦区別しないことで計算量を削減する。移動する回数は \(2\) つの軸を合わせて \(L+R\) 回になる。この場合の数を計算した後に \( {}_{L+R} C_L \) をかければ軸の区別ができる。あとは解説にもある通り、有効な \((L, R)\) の組について足し合わせれば良い。
感想
コンテスト中に解くには時間が足りなかったが、時間をかけても解けなかったので悔しい

コメント