前書き
Codeforces (Div. 2) の最終問題にありがちなグラフ問題がマジで解けないので特訓もかねて記事にしました。
問題概要
\(N\) 頂点の木が与えられる。
木の頂点にはそれぞれ数字が書かれており、頂点 \(i\) には \(a_i\) が書かれている。
ある木の頂点を根にしたときに、「根からどの頂点に至るパスにも、そのパス中に同じ値が2回以上登場しない」という条件を満たす場合、その頂点を「特徴的である」という。特徴的な頂点の数を求めよ。
制約
\(1 \le N \le 2 \times 10^5\)
\(1 \le a_i \le 10^9\)
詳細な解答
※公式解説を翻訳して図を足しています。
ある頂点 \(v\) について考える。さて、\( v \) と同じ値が書かれている頂点があったとする(この頂点を\(u\)と名付ける)。\(v\) を削除したときに複数の連結成分に分かれるが、すべての「特徴的な頂点」は、この時 \(u\) と同じ連結成分内に存在する。
さて、以上のことを、\(v\) からその連結成分の根に向けて有向辺を張ることで表現しよう。そうすると、「頂点が特徴的である」⇄「頂点が全ての有向辺から指されている」という関係が成り立つ。
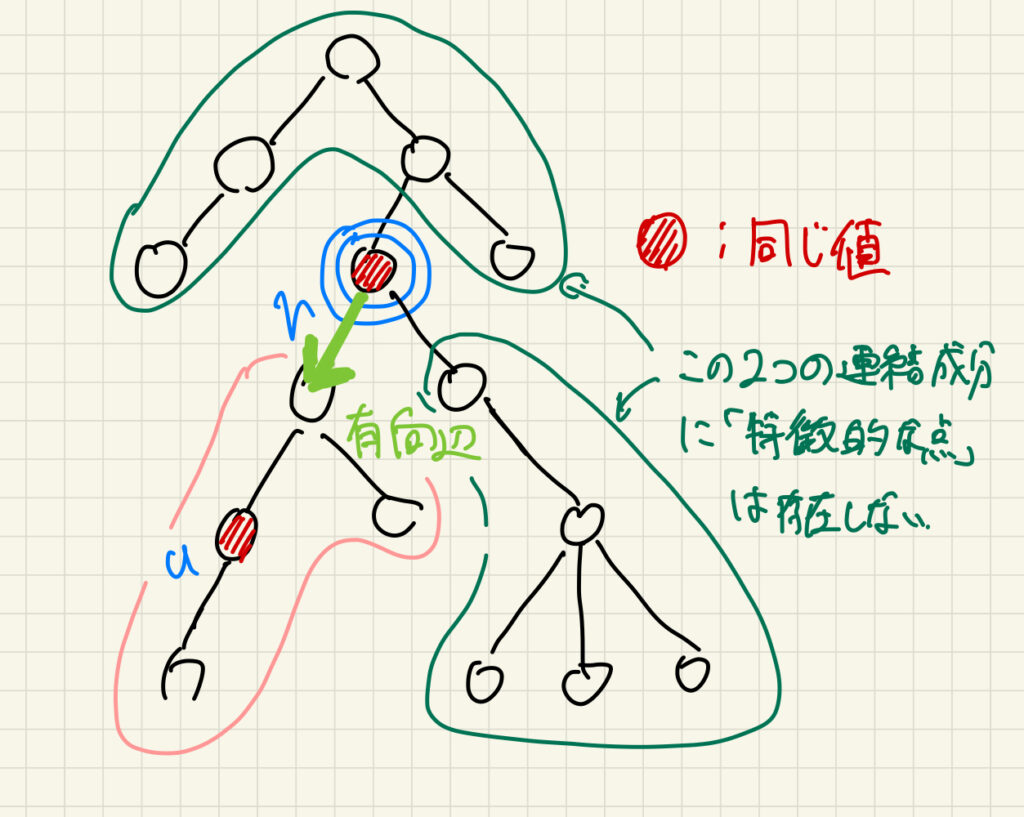
よって、やれば良いことは以下の2つになる。
- 頂点を削除したときに分かれるそれぞれの連結成分内に、その頂点と同じ値が書かれている頂点があるかどうかを判断する
- 有向辺の集合が与えられた時に、全ての有向辺に指されている頂点を列挙する
1番の処理は、オイラーツアーによって木を区間に対応させることで対応可能。部分木を区間に、頂点を区間上の位置に対応させたあと、値ごとに、「その値が書かれている頂点達の区間上の位置」の集合を求め、その中でlower_boundなどにより区間の内部に含まれるかどうかを判定する。自分より子供方向の部分木にしか求められないように見えるが、同じ値を持つ頂点の数を最初に数えておけば、全体から引き算することで親方向の部分木に対しても検出可能。
2番の処理は、全方位木DPによって可能。
反省
解説を読んだ後も、1番の処理も2番の処理も「それをどう実装すんねん」という気持ちになっていた。いろんな手法を知っていかないと応用的なグラフ問題には対応できないと思うのでしっかり抑えたい。
それとは別に、これらの手法を知っていても問題が解けるようになる気がしない……

コメント