前書き
Codeforces に出題されたグラフの問題がまた解けなかったので記事にします。今後 Codeforcesに参加したときに解けなかったグラフ問題は(できるだけ)全部記事にするつもりです。
問題概要
\(N\) 頂点の木が与えられる。
Fib-treeとは、「1頂点のみからなる木」か「頂点数がフィボナッチ数で、1つの辺を削除すると2つのFib-treeに分かれる」のどちらかを満たすものである。
与えられた木がFib-treeであるかどうかを求めよ。
制約
\(1 \le N \le 2 \times 10^5\)
考えたこと
まず \(N\) がフィボナッチ数でなければNOである。
頂点数に関する条件から、\( N = F_i = F_j + F_k \) となる \(j, k\) を考えるが、不等式の評価によればこの組みは \((j, k) = (i-1, i-2)\) に限られる。
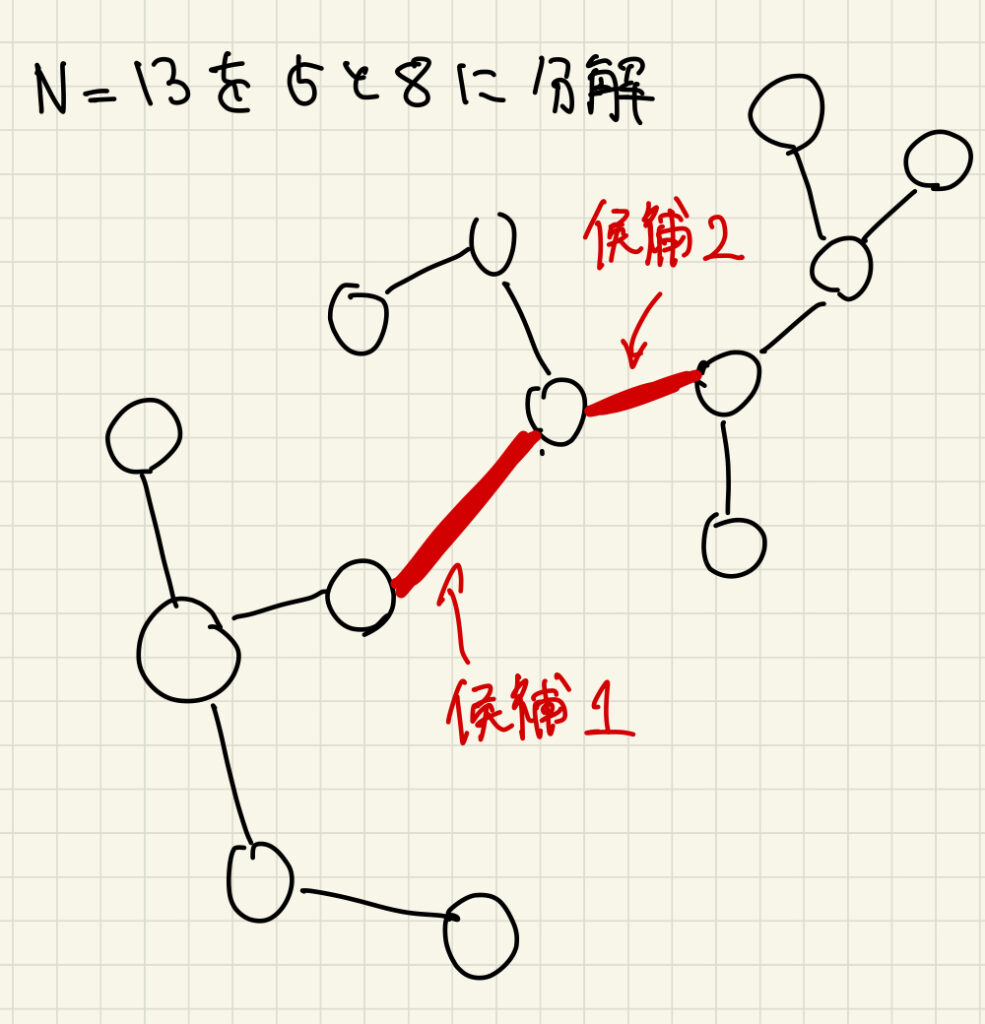
削除する辺の場所を考える必要があるが、候補が \(2\) つ以上ある場合(図1)があり、計算量が減らなくないか?と考えて飛ばした。
詳細な解答
※公式解説を翻訳して図を足しています。
実は、候補が2つ以上ある場合でも、どの辺を切っても良い。(!!)
「頂点数 \(F_i\) のFib-treeのグラフに存在するある辺を削除すると、頂点数 \(F_{i-1}, F_{i-2}\) の2つに分かれるなら、その2つのグラフもFib-treeになる」を証明する。意味が分かりにくいという人は、「頂点数 \(F_i\) のグラフが Fib-tree か判定したいなら、候補となる辺のどっちを切っても良い」と言い換えても良い。(主張していることは同じ。)
証明
\(N\) に関する帰納法による。\(N=2\)の場合は明らかに成立する。
そうでない場合、まず、候補となる辺の数が1つしかない場合も明らかに成立する。
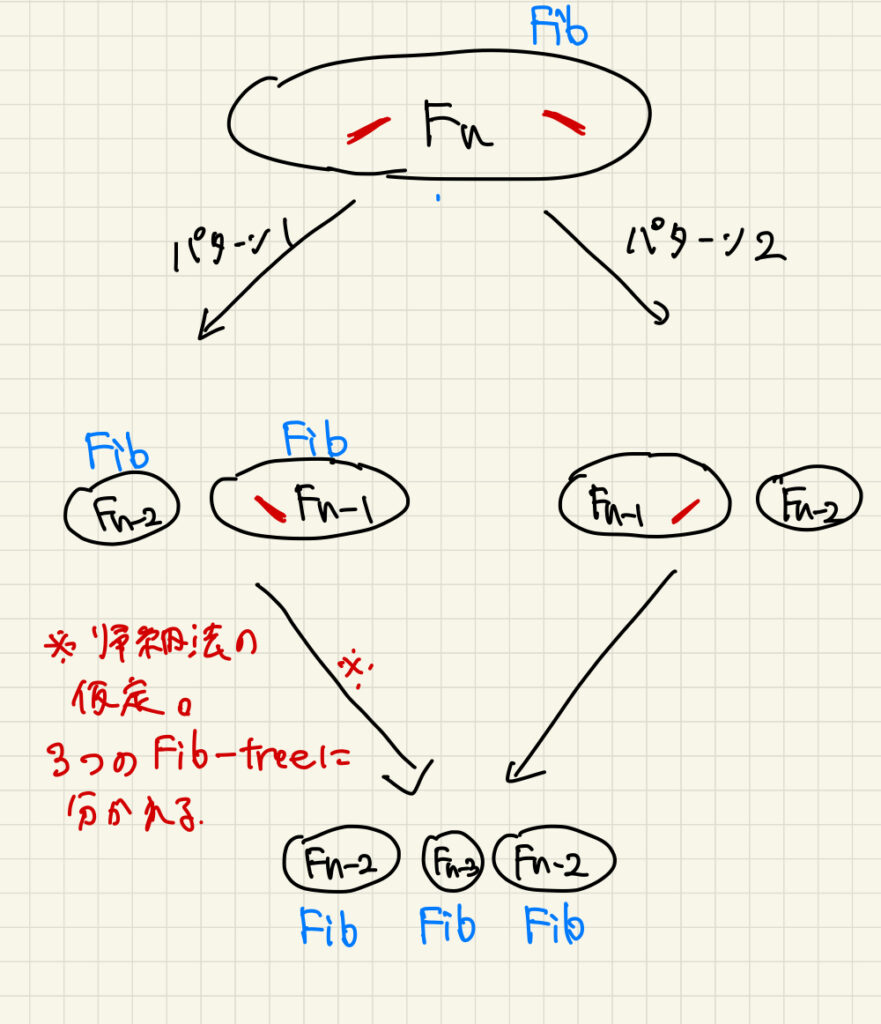
2つ候補がある場合。仮定より、どちらかの切り方では2つのFib-treeに分かれるので、この切り方を「パターン1」とする。証明するべきは、「パターン2の方法で切っても2つのFib-treeに分かれる」である。
パターン1で分かれた2つのグラフのうち、大きい方には先程切らなかった2つ目の候補辺が含まれている。この辺を削除することで、さらに2つのFib-treeに分かれる(帰納法の仮定より)。
パターン2で分かれた2つのグラフに着目する。このとき、大きい方には先程切らなかった1つ目の候補編が含まれていて、この辺を削除すると、結局同じ結果になる。よって、「片方の切り方では2つのFib-treeになるが、もう片方の切り方ではならない」といった状況にはならない。
反省
グラフの問題も苦手だけど、こういう「実は計算量が小さいです〜〜」系の問題もなかなか苦手。普段、問題を解くときから計算量のことを意識していないのが良くないと思う。
あとは証明が苦手だと思う。今回は帰納法を用いて証明する問題だったけど帰納法を用いることすら思い浮かばなかった。

コメント